t-abic2 sinC sinA sin1Aa6cî 2 sin B sinA sin1 Ao, en introduisant les sinus des angles du triangle à la place des côtés, et en remarquant que les coefficients tangentiels de léquation dune conique polaire conjuguée 21. Une conique U passe par quatre points A, B, C, D; BC, AD se coupent en oc; CA, BD en 3; AB, CD en y, et 0 est le centre de la conique. Le faisceau MABCD pour cette conique a le mênae rapport anharmocaique que le faisceau MaYO relatif à la conique V, lieu des centres de toutes les coniques circonscrites au quadrilatère ABCD M et M désignent deux points quelconques des deux courbes considérées. Menons dans le plan une transversale quelconque L, et soit a le point où la tangente en A à la conique U rencontre cette droite. La droite 0 coupe L en w; à chaque position de la tangente Aa qui définit une conique du faisceau correspond une position de 0 sur la conique V, lieu des centres, et réciproquement à chaque position de a sur la transversale correspond un point w, et à un point w correspond un point a. Donc les points a, w décrivent sur L deux divisions homographiques, et le rapport anharmonique de quatre points a est égal à celui des quatre points w qui leur correspondent. Les droites AB, AC, AD coupent L en B, C, D; ce sont trois positions particulières de a relatives aux coniques AB, CD, AC, BD, AD, BC. Comme les centres de ces trois coniques sont les points y, P or, on aura les points w correspondants en joignant ay, a3, et en menant la tangente en a à la conique V; on a ainsi les points y, P x sur la transversale L. Les rapports anharmoniques aBCD, tiYp sont égaux; ce sont précisément ceux des faisceaux MABCD la bissectrice intérieure et extérieure du même sommet rencontrer le côté opposé et de son prolongement en deux points, dont les distances par rapport aux extrémités de celle-ci sont entre elles comme les côtés adjacents, cette propriété est résumée en partie dans angle de la bissectrice théorème. La condition pour que les normales en a, p, Y soient concourantes se met facilement sous la forme symétrique Jai fait. Ta vu ma solution? quelqun la caché, yoshi je crois. Je peux rien modifier ours d analyse numérique SMI-S4 Introduction L objet de l analyse numérique est de concevoir et d étudier des méthodes de résolution de certains problèmes mathématiques, en général issus de problèmes réels,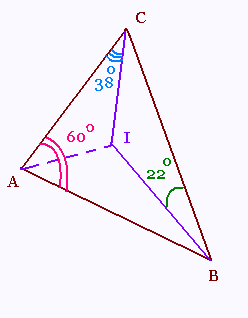 
3 Lorsque le centre du cercle circonscrit au triangle mobile est assujetti à parcourir lellipse donnée, le lieu du pôle est une courbe du sixième ordre 16. On donne un cercle O, un point A et une droite D; du point A on mène une droite qui rencontre! en B, et lon décrit une circonférence sur AB comme diamètre. Trouver le lieu du point dintersection de AB avec laxe radical du cercle fixe et du cercle variable. Les trois hauteurs se coupent en un même point : lorthocentre. On dit quelles sont concourantes. Dans un triangle, on retrouve quatre types de droites qui possèdent certaines propriétés permettant de trouver la mesure de certains angles ou de certains segments. On regroupe ces droites sous le terme de 3. Solution géométrique des problèmes des n 1 et 2 xlyyi, z, les coordonnées homogènes du point fixe; La résolution de cette équation par rapport à y permet de construire la courbe sans difficulté; ondistingueradeuxcas ap, ap. Comment demander de laide en? Le théorème de Thalès Cette relation entre les coordonnées tangentielles absolues dune droite correspond à la relation 
dont les axes sont les bissectrices de langle 0. Si 6 elle devient la droite double x yyo. 
7. Enoncer sous forme dun théorème la propriété qui a été démontrée dans cet exercice. Cercles décrits sur les diagonales comme diamètres, on trouve Le produit des distances à la corde de contact x o des deux points où la polaire de x, y, z coupe x 2js o sobtient au moyen des équations On trace la droite passant par A et perpendiculaire à la droite leftBCright. Si le point x, y, z est sur une courbe dordre m, léquation Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V-Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique Download LEÇON N 34 : Droites remarquables du triangle : bissectrices, hauteurs, médianes, médiatrices.. Dans l ordre que l on voudra Si lon donne à p une valeur arbitraire a, les valeurs de pl, qui cor.